執筆:内橋貴之(名古屋大学)
原子間力顕微鏡法(Atomic Force Microscopy: AFM)は高分子材料の表面構造や力学物性をナノスケール分解能で解析できる手法である
原子間力顕微鏡法(Atomic Force Microscopy: AFM)は様々な環境下(真空・大気・溶液)で高分子材料の表面構造や組成、力学物性(弾性率、粘弾性、凝着力)の分布をナノスケール分解能で可視化したり、力学物性の定量解析ができる手法です。また、高速化技術の進展により、高分子の構造動態をリアルタイムに撮影することも可能になりました。
測定できること
表面構造 / 弾性率 / 粘弾性 / 凝着力 / 力学物性分布 / 構造ダイナミクス
原理
1. AFM技術の概要と基本原理
ナノメーターサイズの尖った針を試料に近づけて、針先と試料の間の何らかの物理量を検出し、その分布をマッピングする顕微鏡は走査型プローブ顕微鏡(Scanning Probe Microscopy: SPM)と総称され、検出する物理量に応じて様々な種類があります。最初のSPMである走査型トンネル顕微鏡(Scanning Tunneling Microscopy: STM)
1)は、金属針と導電試料の間に流れるトンネル電流を検出することで、固体表面の原子構造を実空間で可視化することが出来ます。STMの出現によってナノサイエンスが爆発的に発展したことから、発明者のBinningは1986年にノーベル物理学賞を受賞しました。STMは電流を検出するために試料に導電性が必要ですが、この欠点を克服するために原子間力顕微鏡(Atomic Force Microscopy: AFM)が同じくBinningらによって発明されました
2)。AFMは試料の導電性を問わないことに加え測定環境を選ばないことから、金属から有機材料、生体高分子まで様々な対象を真空、大気、溶液中といったあらゆる環境下で測定することができます。
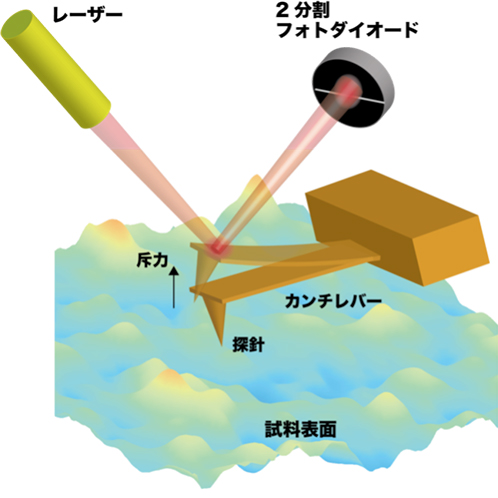 図1 AFMの原理
図1 AFMの原理
AFMの探針はカンチレバーと呼ばれる小さな板バネの先端に取り付けられており、探針と試料の間に働く力はカンチレバーのたわみ(変位)を通じて検出されます。つまり、図1のように探針が斥力を受けるとカンチレバーは試料反対側に変位し、引力を受けると試料側に変位します。カンチレバーの微小な変位を検出するために様々な方法が提案されてきましたが、光てこ法が最も簡便でかつ高感度なためよく使われています。光てこ法では、カンチレバーの背面に斜めからレーザー光を照射し、その反射光の位置変化を二分割したフォトダイオードに入射します。カンチレバーの変位に比例して反射光がフォトダイオードに入射する位置が上下するので、二分割されたフォトダイオードの光量差が変化します。このような単純な方法でも意外に高感度なカンチレバー変位の検出が可能で、1 nm以下の変位を容易に検出することができます。さて、探針を試料に接触させた状態、つまりカンチレバーが反った状態で、試料と探針の位置を2次元に相対的に動かすと、試料の表面構造に応じてカンチレバーの変位も変化します。従って、探針をラスター走査しながら各ピクセル位置でのカンチレバーの変位を記録すれば、試料の表面構造を画像として構成することができます。しかしこの方法では、表面の凹凸が粗く高さが大きく変化するような試料では、探針が試料表面から離れてしまったり、柔らかい試料だと探針が試料を破壊してしまいます。そのため、単にカンチレバーの変位を記録するのではなく、変位(つまり探針と試料の間に働く斥力)が一定になるように、フィードバック制御(通常、積分(I)と比例制御(P)が使われます)により試料を上下させます(図2)。このフィードバック制御の出力を2次元にマッピングすることで、探針から試料にかかる力を一定に制御した状態で表面構造の画像を作ることができます。AFMの空間分解能は、探針が感じる試料からの力学相互作用の領域に依存するので、基本的には探針先端のサイズで決まります。比較的容易に水平方向で2 nm以下、垂直方向で0.1 nm以下の分解能が得られますが、先端が原子レベルで先鋭であれば原子分解能での表面構造解析も可能です。
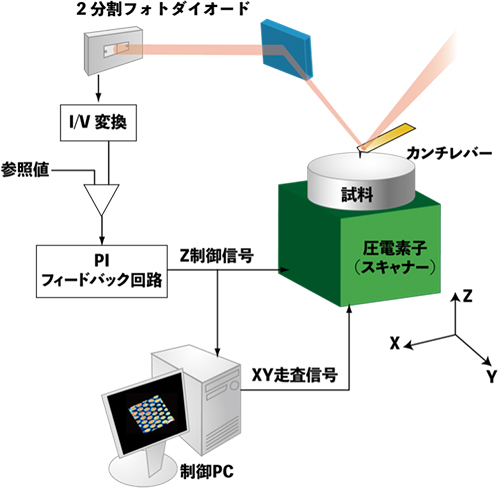 図2 AFMの装置構成概要
図2 AFMの装置構成概要 2. タッピングモード
上述したのはコンタクトモードと呼ばれる最初期の最も単純な測定モードですが、AFMには多数の測定モードが提案されており、今日ではコンタクトモードが使われることはあまりありません。容易に想像できますが、コンタクトモードでは探針を試料に接触して走査するので、探針先端あるいは試料が摩擦によりダメージを受けてしまいます。さらには、基板に弱く吸着した分子などは走査によって探針に引きずられてしまいます。探針による試料へのダメージを軽減するために考案されたのがタッピングモードと呼ばれる測定法です
3)。タッピングモードでは圧電素子によりカンチレバーを機械共振周波数で振動させます。探針が試料に接触するとカンチレバーの振動振幅は減少し、探針を試料に押し付けていくと振動振幅はさらに減少していきます。このことから、振動振幅の減少率は試料表面の高さ(凹凸)に依存します。振動振幅をある程度減少させた状態を維持しながらラスター走査することで、コンタクトモードと同様に表面構造を可視化することができます(図3)。コンタクトモードとの違いは、タッピングモードでは探針が試料に間欠的に接触することで、走査による探針から試料への水平方向の力、つまり摩擦力を大幅に軽減できることです。また、タッピングモードでは針と試料の接触力はカンチレバーの過渡応答特性に依存して変化します。カンチレバーの共振特性を示す物理量としてQ値があり、Q値が大きいほど共振特性がシャープになります。大まかに言って接触力はカンチレバーのQ値に反比例します。真空中や大気中などダンピング効果が低く、カンチレバーのQ値が高い環境(大気中で数百、真空中で数千〜数万)では接触力をかなり小さくすることができます。
 図3 タッピングモードの原理
図3 タッピングモードの原理
タッピングモードはカンチレバーの振幅を検出することから振幅変調(Amplitude Modulation: AM)モードとも呼ばれます。一方、針と試料の間に働く力に応じてカンチレバーの共振周波数は変化する(引力が働くと共振周波数は低下し、斥力では高くなります)ことから、周波数変化が一定になるようにフィードバック制御して表面構造を可視化するモードは周波数変調(Frequency Modulation: FM)モードと呼ばれます
4)。FMモードではAMモードに比べて高感度に力検出が可能とされており、ベンゼン環の骨格や分子の化学結合まで可視化した超高解像な観察に利用されています
5)。
3. 位相検出による物性コントラスト
タンピングモードでは表面構造に加えて試料の力学物性分布も画像化することができます。強制振動させたカンチレバーの先端にある針が試料に接触すると、振動振幅は減少すると同時に振動の位相も変化します。カンチレバー先端に斥力が加わると共振周波数が高くなるので振動周波数での位相は進むことになります(図4)。ある位置での位相を基準として、試料表面がそれより硬い場所では位相が進み、柔らかい場所では共振周波数が低くなるので位相は遅れます。従って、カンチレバーの励振信号を参照信号として、カンチレバー振動の位相シフトをマッピングすることで、硬さ(弾性率)の相対変化をコントラストとして画像化でき、表面構造との対応を調べることができます。カンチレバーの位相変化には弾性率の変化以外にも、エネルギー損失による位相遅れも反映されるので、高分子材料のような粘弾性特性を持つ試料では位相のコントラストにその影響も含まれます。さらに言えば、振動している探針が試料から離れる際に凝着力が働くと位相が遅れるので、凝着力の局所分布も位相像に反映されます。
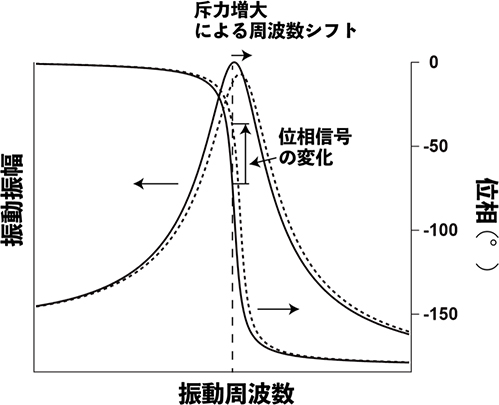 図4 カンチレバーの共振特性と周波数シフトによる位相信号の変化
図4 カンチレバーの共振特性と周波数シフトによる位相信号の変化
このように、位相像の解釈は単純ではなく定量的な解析は困難ではありますが、例えばブレンドポリマーなどの二種類以上の異なる力学物性を持つ材料から構成される試料で、表面構造に見られない明確なコントラストが位相像では得られることから(図5)、材料の空間分布など定性的解析には有用な測定モードです。
 図5 スチレン−ブタジエン−スチレン(SBS)トリブロックコポリマーの表面凹凸像と位相像
図5 スチレン−ブタジエン−スチレン(SBS)トリブロックコポリマーの表面凹凸像と位相像
4. 力学特性計測とマッピング
AFMで探針と試料に働く力の距離依存性は最も基本となる計測量で、フォースカーブと呼ばれます。フォースカーブは、探針と試料の距離制御を行う圧電素子の移動量を横軸に取り、カンチレバーの変位量を縦軸にプロットします(図6)。カンチレバーのばね定数kがわかっていれば、変位は簡単に力(N)に換算できます。フォースカーブは探針と試料を近づけていく方向(アプローチ)と離していく方向(リリース)の両方向が記録され、斥力相互作用をY軸正方向に取る場合が多いです。従って、探針と試料を近づけていき、最終的に接触すると斥力が働き、押し込みに応じて斥力が増加します。試料表面がカンチレバーのばね定数に比べて十分硬い場合には、カンチレバーの変位と圧電素子の変位は一致するはずです。一方、カンチレバーのばね定数に比べて試料が柔らかいと、探針の押し込みにより試料表面が変形するのでカンチレバーの変位と圧電素子の移動量は一致しなくなり非線形になります。この関係から試料の局所弾性率を評価することができます。弾性率の定量値を算出するためには探針と試料表面の接触面積を知る必要がありますが、現実的にはこれを実測することは不可能です。通常は探針先端の形状を球と仮定した接触モデルの理論計算式をフォースカーブにフィッティングし、そのフィッティングパラメーターから弾性率を得ます。接触モデルとして、斥力のみを考慮したHertzモデル、凝着効果を取り入れたJKRモデルやDMTモデル等がよく知られており
6)、試料や環境に応じて使い分ける必要がありますが、多くの場合JKRモデルが採用されています。次に、探針と試料間の距離を離していくと斥力は減少していきます。この際、試料に粘弾性がある場合、斥力変化は探針を試料に接近させた時の曲線と一致しません、つまり、ヒステリシスを示します。このヒステリシスの面積は粘弾性による散逸エネルギーに相当します。最終的に、探針が試料から離れる際に凝着力があると探針が試料に引っ張られるので、大きな引力が働きます。このように、フォースカーブから局所位置での弾性率やエネルギー散逸、凝着力を定量的に計測することができます。また、フォースカーブを二次元の各ピクセル位置で取得し、各ピクセル位置での力学特性をマッピングすることも可能です。これはフォースボリュームモードと呼ばれ、これにより表面構造と力学特性分布との相関を調べることができます
7)。
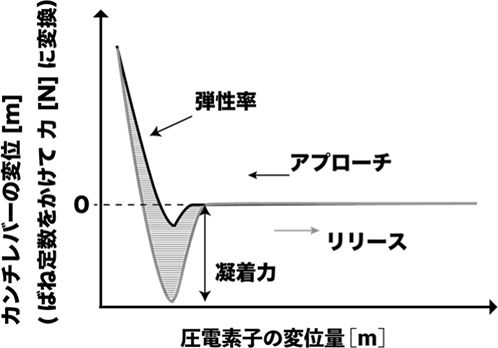 図6 フォースカーブと力学特性
図6 フォースカーブと力学特性5. ダイナミクス計測
通常のAFMでは画像取得に数分の時間が必用なため、この時間スケールで試料が静止している必要があります。つまり、構造ダイナミクスを伴う現象を観察することは困難です。最近、AFMの画像取得速度が大幅に改善された高速AFM技術が開発され、1秒以下の撮像速度でAFM測定が可能になりました。高速AFMでも位相検出やフォースボリューム計測が可能なので、高分子の構造と同時に力学特性のダイナミクスも撮影できます。高速AFMを高分子試料に応用した例はまだ多くありませんが、超分子ナノファイバーの重合過程
8)やゲル微粒子の温度依存的な収縮過程の観察(図7)
9) 10)などが報告されており、今後、高分子のダイナミクス観察の研究例が増えることが期待されます。
 図7 ハイドロゲル微粒子の昇温収縮過程
図7 ハイドロゲル微粒子の昇温収縮過程
参考文献
1) Binning, G.; Rohrer, H.; Gerber, C.; Weibel, E. Surface Studies by Scanning Tunneling Microscopy. Phys. Rev. Lett. 1982. https://doi.org/10.1103/PhysRevLett.49.57.
2) Binnig, G.; Quate, C. F.; Gerber, C. Atomic Force Microscope. Phys. Rev. Lett. 1986, 56 (9), 930–933. https://doi.org/10.1103/PhysRevLett.56.930.
3) Zhong, Q.; Inniss, D.; Kjoller, K.; Elings, V. B. Fractured Polymer/Silica Fiber Surface Studied by Tapping Mode Atomic Force Microscopy. Surf. Sci. 1993, 290 (1–2), L688–L692.
https://doi.org/10.1016/0039-6028(93)90582-5.
4) Albrecht, T. R.; Grütter, P.; Horne, D.; Rugar, D. Frequency Modulation Detection Using High-Q Cantilevers for Enhanced Force Microscope Sensitivity. J. Appl. Phys. 1991.
https://doi.org/10.1063/1.347347.
5) Gross, L.; Mohn, F.; Moll, N.; Liljeroth, P.; Meyer, G. The Chemical Structure of a Molecule Resolved by Atomic Force Microscopy. Science (80-. ). 2009. https://doi.org/10.1126/science.1176210.
6) Jee, A. Y.; Lee, M. Comparative Analysis on the Nanoindentation of Polymers Using Atomic Force Microscopy. Polym. Test. 2010. https://doi.org/10.1016/j.polymertesting.2009.09.009.
7) Wang, D.; Fujinami, S.; Nakajima, K.; Inukai, S.; Ueki, H.; Magario, A.; Noguchi, T.; Endo, M.; Nishi, T. Visualization of Nanomechanical Mapping on Polymer Nanocomposites by AFM Force Measurement. Polymer (Guildf). 2010. https://doi.org/10.1016/j.polymer.2010.03.052.
8) Fukui, T.; Uchihashi, T.; Sasaki, N.; Watanabe, H.; Takeuchi, M.; Sugiyasu, K. Direct Observation and Manipulation of Supramolecular Polymerization by High-Speed Atomic Force Microscopy. Angew. Chemie - Int. Ed. 2018, 57 (47), 15465–15470. https://doi.org/10.1002/anie.201809165.
9) Matsui, S.; Nishizawa, Y.; Uchihashi, T.; Suzuki, D. Monitoring Thermoresponsive Morphological Changes in Individual Hydrogel Microspheres. ACS Omega 2018, 3 (9), 10836–10842. https://doi.org/10.1021/acsomega.8b01770.
10) Nishizawa, Y.; Matsui, S.; Urayama, K.; Kureha, T.; Shibayama, M.; Uchihashi, T.; Suzuki, D. Non-Thermoresponsive Decanano-Sized Domains in Thermoresponsive Hydrogel Microspheres Revealed by Temperature-Controlled High-Speed Atomic Force Microscopy. Angew. Chemie Int. Ed. 2019, 1–6. https://doi.org/10.1002/anie.201903483.
分析例・プロトコール






