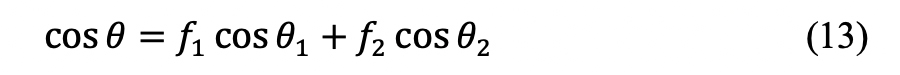執筆:宮田隆志(関西大学)
高分子材料の表面性質(親水・疎水性、ぬれ性)を評価する簡便な方法
接触角測定では、高分子材料の表面に液体を接触させ、その液滴表面と材料表面とのなす角(接触角)を測ります。一般に液体として水が用いられ、その接触角から高分子材料表面の親水・疎水性を評価できます。接触角は高分子材料と液体の表面張力(表面自由エネルギー)によって決まりますので、表面張力が既知の液体を用いると高分子材料の表面自由エネルギーを求めることができます。表面分析法の中で最表面の性質を評価できる汎用的方法です。
測定できること
接触角 / 表面張力 / 表面自由エネルギー / 親水性・疎水性 / 撥水性 / ぬれ性
原理
1. はじめに
高分子材料の表面は、その内部構造とは異なっており、置かれている環境によって大きく影響されます。また、高分子材料の表面性質はその物性や機能を左右するため、表面の構造や性質を分析することが不可欠です。高分子材料の表面分析法としては、X線光電子分光法(X-ray Photoelectron Spectroscopy: XPS)やフーリエ変換赤外分光法(Fourier Transform Infrared Spectroscopy: FT-IR)の全反射測定法(Attenuated Total Reflection: ATR)などが利用されていますが、表面からある程度の深さを含んだ情報しか得ることができません。それに対して、接触角測定では高分子材料の最表面の情報を得ることができ、表面分析法としては最も汎用的な方法として広く利用されています。以下に接触角測定の基礎とその活用について説明します
1)2)。
2. 接触角測定の原理
固体表面に液滴を落とすと、固体の表面張力
γSと液体の表面張力
γL、固体と液体の界面張力
γSLが釣り合ってある角度(接触角)
θになります(図1)。このとき、固体と液体、空気の境界点Aにおける力の水平成分の釣り合いから、次式のYoungの式が得られます。
ここで、垂直方向の力の釣り合いは固体の凝集力によって維持されますので通常は考える必要がありません。しかし、固体表面が軟らかい場合や液体によって膨潤する場合には、縦成分の力によって表面形状が変化するために接触角が高くなりますので、表面の化学的性質を評価する場合には注意が必要です
3)。
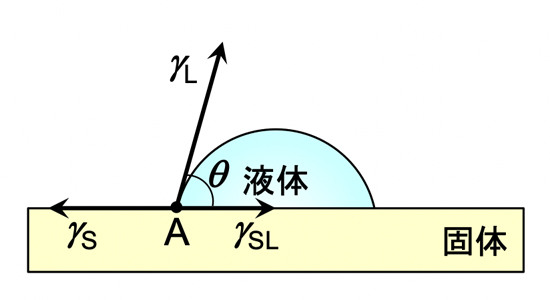 図1 高分子材料表面における液滴の接触角
図1 高分子材料表面における液滴の接触角
接触角測定に用いられる液体として一般に水が利用されており、親水性表面で
θは小さく、疎水性表面では大きくなります。このように接触角測定では高分子材料表面の化学的性質を評価できますが、その表面は平坦であることが前提です。表面に凹凸がある場合にはその物理的構造(表面粗さ)が接触角に影響するため、化学的性質を客観的に評価することは難しくなります。また、水以外の液体を用いることもでき、高分子材料表面における液体のぬれ性も評価できます。通常の接触角測定では、高分子材料の表面上に液滴を静置している状態が基本となります。一般に、シリンジなどを用いて液滴を材料表面に静かに接触させますが、その液適量は一定にして数カ所での測定を行うことが推奨されます。また、接触角は温度や湿度などにも影響されるので測定する環境には注意するべきです。
高分子材料の表面は動的な場合が多く、その動的な表面構造の変化を接触角で追跡することも可能です。たとえば、高分子材料表面に液滴を置いて、その接触角の経時変化をモニターすることにより表面の動的変化を調べることができます。また、シリンジなどで液体を固体表面に接触させた後、液滴を膨らませたり、吸い込んだりすることにより、液滴界面が固体表面を前進および後退するときの接触角(前進接触角、後退接触角)を測定する方法も利用されています。平坦で静的な表面でも前進接触角と後退接触角は異なることが多いのですが、この値が大きく異なる場合には表面の動的変化や物理的な凹凸が影響していることが多いので注意が必要です。
ここで、表面張力と密接に関連する表面自由エネルギーについて簡単に説明しておきます。まず、液体の場合には、その表面張力は表面に平行に、液面上の単位長さの線に直角にはたらく応力として定義されており、表面自由エネルギーは表面が持つ過剰の自由エネルギーとして定義されています
4)。したがって、表面張力は単位mN/mをもつベクトル量であるのに対し、表面自由エネルギーは単位mJ/m
2のスカラー量になります。しかし、J=N•mよりmN/m=mN•m/m
2=mJ/m
2となりますので、表面張力と表面自由エネルギーの単位は同じで、それらの絶対値も同じ値になります。いずれに対しても
γという記号が用いられます。また、
γを表面自由エネルギーとして取り扱い、高分子材料と液体との接触界面の自由エネルギー変化が極小値となる条件で解くと、Youngの式を導くこともできます。
3. 接触角とぬれ性
固体表面に液滴を静置すると、固体表面が液体表面に置き換えられます。この現象を“ぬれ”といいます。固体と液体の表面自由エネルギーとその間の界面自由エネルギーのバランスによって液体の広がり方(ぬれ性)は決まります。固体表面のぬれは材料の親水・疎水性と関連し、接着や粘着などの表面・界面に関わる材料分野では重要な性質です。このようなぬれの尺度として拡張ぬれ仕事
Wsが用いられています。
WS ≥0の時に、液体は固体表面を広がってぬらすことができます。また、式(2)とYoungの式(式(1))から次式が得られます。
この式から、
Ws = 0は
θ= 0となった状態であり、固体表面が完全に液体表面に置き換えられることになります。したがって、
θが小さくなるほどぬれている状態であることがわかります。
WS ≥0の条件になる高分子材料と液体の組み合わせで接触角測定を行うと、拡張ぬれが起こって常に
θ = 0となってしまいます。そのため、高分子材料表面の化学的性質を評価するためには、
WS <0の条件となる液体を用いて接触角測定を行う必要があります。しかし、実際にはこの条件を正確に調べてから接触角測定を行うことは難しいので、一般的には高分子材料の
γSよりも大きな
γLの液体で接触角測定を行うようにすると、拡張ぬれとなる条件を避けることができます。そのため、接触角測定には水やジヨードメタンなどの
γLが大きな液体が用いられます。逆に、
γLが小さな液体を用いると拡張ぬれの条件になりやすいので注意が必要です。たとえば、大きな
γSをもつガラス表面に小さな
γLのベンゼンの液滴を落とすとベンゼンはぬれ拡がり、接触角を測定することはできません。高分子材料と液体との親和性を評価するために接触角を利用する場合も見受けられますが、上記のガラスとベンゼンの組み合わせのように親和性が低くても拡張ぬれの条件になると
θ = 0になるので注意してください。
4. 臨界表面張力による評価
表面張力が異なる様々な液体を用いて高分子材料表面で
θを測定すると、液体の
γLとcos
θとの間には明確な直線関係が存在します(図2)。この直線をcos
θ = 1 (
θ = 0)に外挿したときの
γLの値は、この高分子材料の臨界表面張力
γCと定義されています
5)。
γCを求めるための図2はZismanプロットと呼ばれています。Zismanプロットのための液体としては、飽和炭化水素などの同族な液体が用いられ、アルコールや脂肪酸など同族の異なる液体が用いられた場合には直線関係から外れてくることもあります。
.jpg) 図2 n-アルカンの表面張力とポリテトラフルオロエチレン上での接触角との関係(Zismanプロット)
図2 n-アルカンの表面張力とポリテトラフルオロエチレン上での接触角との関係(Zismanプロット)
図2からわかるように、高分子材料の
γCよりも小さな表面張力の液体は常に
θ = 0となりますので、自発的に広がってその高分子材料を完全にぬらすことになります。したがって、
γCの大きな高分子材料は多くの液体にぬれやすく、
γCの小さな高分子材料はぬれにくいということになります。このように
γCは固体のぬれ性の指標となりますので、
γCを高分子材料の
γSとみなして議論する場合もあります。表1に代表的な高分子表面の臨界表面張力を示します
6)。表1から、フルオロカーボン系高分子の臨界表面張力が全体的に低く、表面がぬれにくいことがわかります。
表1 高分子材料の臨界表面張力と表面張力の各成分の算出例(単位mN/m,20℃)
.jpg)
5. 界面自由エネルギーの取扱による評価
接触角からは高分子表面と液体の表面張力や界面張力の関係を知ることができます。既知の
γLをもつ液体を用いて接触角を測定すると臨界表面張力を求めることができますが、Zismanプロットを描くために多数の液体で接触角測定を行う必要があります。一方、高分子材料と液体との
γSLを何らかの方法で求めることができれば、Youngの式から
γSを決定することができます。しかし、
γSLを測定することが難しいため、
γSと
γLから
γSLを求める様々な理論式が提案されてきました。
同一分子(分子1,2)同士の相互作用エネルギー
E11、
E22を用いて、分子1と分子2の間の相互作用エネルギー
E12を記述することにより、
γ12も
γ1と
γ2を用いて表すことが検討されてきました。その際、表面自由エネルギーは、分散力成分や極性成分、水素結合成分などの分子間力に基づく各成分に分けることができ、2種類の材料の分子に働く相互作用エネルギーは各成分同士で働くと仮定していくつかの理論が提案されています。表2に代表的な理論式をまとめておきます。各理論の特徴は、表面自由エネルギーの成分分けの方法と、異分子の接触による効果に対して幾何平均あるいは調和平均のいずれを選ぶかの違いです。
表2 界面自由エネルギーの理論式
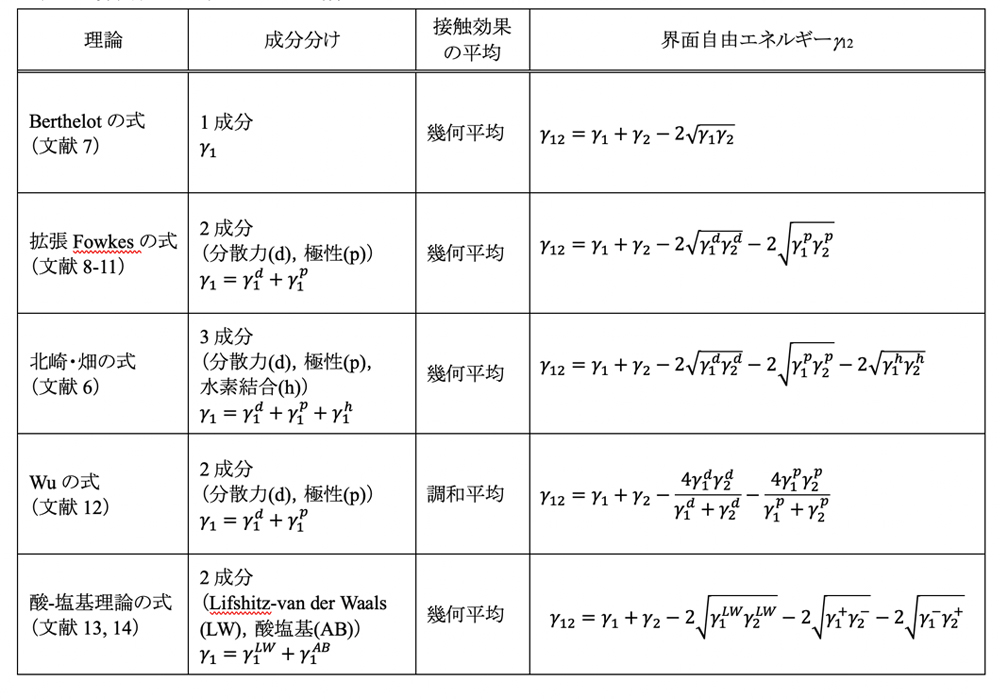
いずれの理論式も界面自由エネルギーを各材料の表面自由エネルギーで表しています。そこで、材料1,2を高分子材料Sと液体Lに置き換えて
γ12を
γSLにすると、Youngの式は
γSと
γL、
θで表すことができます。したがって、
γLが既知である液体を用いて接触角測定により
θを求めると、高分子材料の
γSを算出できます。一般的な接触角測定装置では、表面自由エネルギー解析ソフトが導入されており、上記のような界面自由エネルギーの取り扱いについて選択項目があります。2成分分けであれば2種類の液体、3成分分けであれば3種類の液体を用いて接触角測定を行い、各接触角の値を入力することにより高分子材料の表面自由エネルギーを算出できます。装置付属の解析ソフトを利用する場合には、上記のような仮定を知った上で理論式を選択する必要があります。また、上記のような成分分けそのものに否定的で、表面自由エネルギーをエンタルピー項とエントロピー項に分けるべきであるという意見もあります
15)。ただし、これまで数多くの研究で拡張Fowkesの式などが活用されており、その有用性についても報告されています
16)。
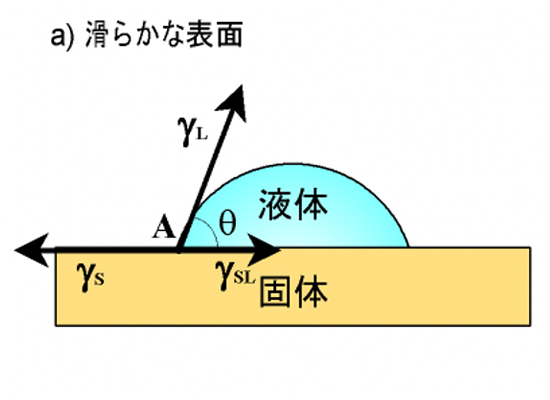
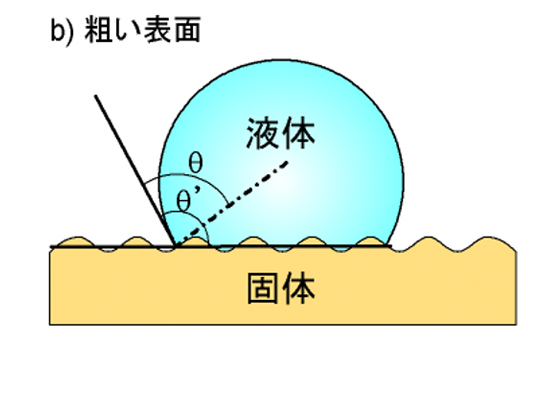
6. 表面粗さ・不均一性の影響
通常、平坦な高分子材料表面で接触角を測定しますので、接触角測定では表面の化学的性質を評価できます(図3(a))。しかし、凹凸があるような粗い表面の場合には、その凹凸による実際の面積を考慮した補正が必要になります(図3(b))。そのような場合には、見かけの面積に対する実面積の比
r(
r >1)を用いた次のようなWenzelの式が利用されます
17)。
ここで、
θroughと
θsmoothは同じ材料と液体の組み合わせで表面が平坦な場合と粗い場合の接触角を示しています。高分子材料の表面に凹凸がある場合にはrが大きくなり、Wenzelの式から液体のぬれやすさは次のようになります。
i)
θsmooth < 90°のとき、
θrough <
θsmoothになり、一層ぬれやすくなる。
ii)
θsmooth > 90°のとき、
θrough >
θsmoothになり、一層ぬれにくくなる。
このような粗い表面では前進接触角と後退接触角に大きな差があり、接触角履歴(ヒステリシス)が生じます。
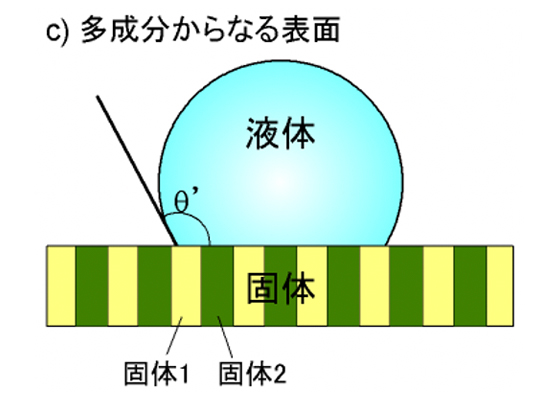
また、高分子材料では多成分からなる場合も多く、そのような複合表面に対してCassieの接触角が提案されています(図3(c))
18)。例えば、成分1と2からなる二成分系の高分子材料表面での
θは、各成分単独の
θ1、
θ2と各成分が表面を占める割合
f1、
f2によって次式のCassieの式で表すことができます。
このように粗い表面や不均一な表面での接触角測定では注意が必要です。逆に、大きな表面積を有するフラクタル表面では水滴の見かけの接触角
θ =174°となって超撥水性を示すことが報告されており、水滴をはじく表面の設計が試みられています
19)。また、凹凸のある高分子材料表面では、その角張った角に液滴の端が存在するときにぬれのピン止め効果が現れます
20)。Youngの式などはいずれも熱力学的平衡状態の式ですが、ぬれのピン止め効果の場合には熱力学的平衡状態ではなく、準安定状態として高い接触角を示していると考えられます。
参考文献
1) 宮田隆志,接着と界面化学,接着ハンドブック第4版(日本接着学会編),日刊工業新聞社,31-55 (2007).
2) 宮田隆志,接着と界面化学,プロをめざす人のための接着技術教本(日本接着学会編),日刊工業新聞,1-22 (2009).
3) A. Carre, J.-C. Gastel, M. E. R. Shanahan, Nature, 379, 432 (1996).
4) 岩波 理化学辞典 第5版,岩波書店 (1998).
5) W. A. Zisman, “Contact Angle, Wettability and Adhesion” (Advances in Chemistry Series, No. 43), Am. Chem. Soc., 1 (1964).
6) 北崎寧昭,畑 敏雄,日本接着学会誌, 8, 131 (1972).
7) D. Berthelot, Comp. Rend., 126, 1703 (1898).
8) F. M. Fowkes, “Contact Angle, Wettability and Adhesion” (Advances in Chemistry Series, No. 43), Am. Chem. Soc., P. 99 (1964).
9) D. K. Owens, R. C. Wendt, J. Appl. Polym. Sci., 13, 1741 (1969).
10) D. K. Owens, R. C. Wendt, J. Appl. Polym. Sci., 14, 1725 (1970).
11) D. H. Kaelble, K. C. Uy, J. Adhesion, 2, 50 (1970).
12) S. Wu, J. Polym. Sci., C34, 19 (1971).
13) R. J. Good, "Contact Angle, Wettability and Adhesion", Ed. K. L. Mittal, VSP , P.3 (1993).
14) C. J. van Oss, M. K. Chaudhury, R. J. Good, Chem. Rev., 88, 92 (1988).
15) 井本稔,表面張力の理解のために,高分子刊行会 (1992).
16) 角谷賢二,泰井俊明,中前勝彦,松本恒隆,日本接着協会誌, 18, 345 (1982)).
17) R. N. Wenzel, Ind. Eng. Chem., 28, 988 (1936).
18) A. B. D. Cassie, S. Baxer, Trans. Faraday Soc., 40, 546 (1944).
19) K. Tsujii et al., Angew. Chem. Int. Ed., 36, 1011 (1997).
20) P. G. de Gennes, F. Brochard-Wyart, D. Quere, “Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves”, Springer, Chapter 9 (2003).
分析例・プロトコール




.jpg)
.jpg)