執筆:山本勝宏 (名古屋工業大学)
小角散乱法は、測定対象試料中の散乱長密度揺らぎを計測し、溶液中の高分子の広がり、ミセルの構造、ミクロ相分離構造などナノメートスケールの構造を非破壊で観測する手法
小角散乱法は、測定対象試料中の散乱長密度(中性子の散乱長密度、原子散乱因子(電子密度))の空間的な揺らぎ(構造)により散乱される中性子(X線)の干渉を計測し、溶液中の高分子の広がり、水溶液中でのタンパク質のサイズや形状、ミセルの構造(サイズや形状、その分布)、ミクロ相分離構造(周期、モルフォロジー)、結晶ラメラ、ゲルの網目構造、ナノ粒子の凝集状態などに関するナノメートスケールの構造を非破壊で観測する手法です。
測定できること
ナノメートルスケールの構造 / 粒子径 / 粒径分布 / 粒子形状 / ミクロ相分離構造 / 液晶構造 / ゲルの網目 / 不均一性 など
原理
はじめに
小角散乱は、散乱角(2θ)が数°以下の散乱波を測定する手法であり、波長をλとするとBraggの法則(λ=2
dsinθ)から、より小さな散乱角で測定することは、大きな構造(
d)を観測することを意味します。散乱角が1mrad~0.1rad程度が通常の測定範囲(散乱ベクトルの大きさで表現すれば、波長0.15nmのとき
q = 0.04 ~ 4 nm
-1)で観測される実空間の構造の大きさは、数nmから数100nmとなります。この範囲の大きさに対応する高分子やソフトマテリアルの構造としては、溶液中の高分子の広がり、鎖状高分子の持続長や局所コンフォメーション、粒状タンパク質、ミセルの形状・大きさ、ミセルの集合体、濃厚、準希薄溶液あるいはゲル中でのセグメント分布の相関長、結晶性高分子のラメラ厚、ラメラ間距離、ブロック共重合体のモルフォロジーやその周期の大きさ、高分子材料中のフィラーの構造・分散状態などが挙げられます。ナノメートルオーダーの構造観測手法としては、実空間観察法としての透過型電子顕微鏡(TEM)や原子間力顕微鏡(AFM)も有力なツールですが、これらは超薄切片や表面の局所構造に限られているのに対し、小角散乱法は中性子(X線)の高い透過力によって内部構造を非破壊に観測できます。さらに、陽子加速器(や放射光)など大型施設の利用により短い時間での時間分割測定も可能になりました。さらに試料回りの自由度が高く、温度、圧力、調湿環境、様々な他の分析手法との同時測定、成型加工プロセス中での構造変化(in-situ)の追跡、デバイスの動作状態で測定(オペランド測定)などが可能であることが大きな長所です。
中性子散乱では試料中の原子核ごとの散乱長(Scattering Length)の揺らぎ(分布)を観測することになります。特にソフトマテリアルの構造解析に用いるときは、水素原子を多く含む系となるため(高分子、炭化水素溶媒や水中での構造観測)、しばしば重水素化物を用いてコントラストを付けます。これは、水素原子の散乱長
bが軽水素と重水素で大きく異なるためです。表に軽水素(H)と重水素(D)の散乱長、および散乱断面積σの値を記します。また干渉性の散乱断面積と非干渉性の散乱断面積を持つことも特徴であります。前者は興味の対象である構造として現れ、後者は一般的には特徴のないバックグラウンド信号を与えることとなります。表に示す通り、水素は非常に大きな非干渉性の散乱断面積を持つことが分かります。したがって、軽水素を多く含む試料においては、バックグラウンドが高くなるため、重水素化物の割合を増やすことは測定における一つの条件となります。
表1 原子の散乱長と散乱断面積
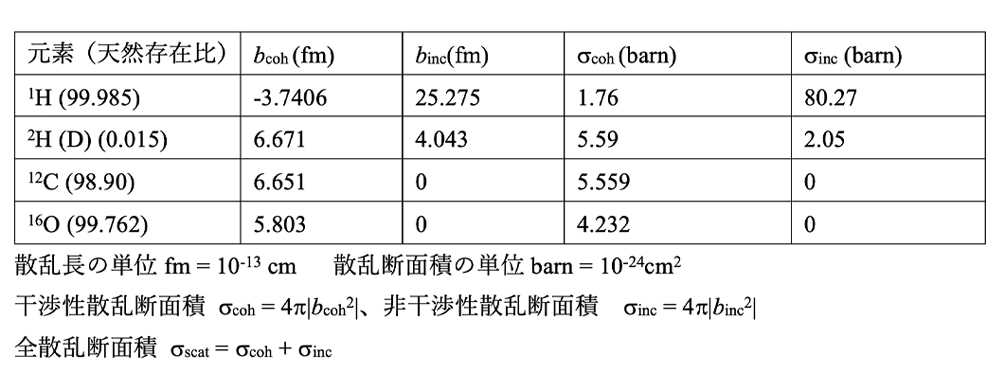
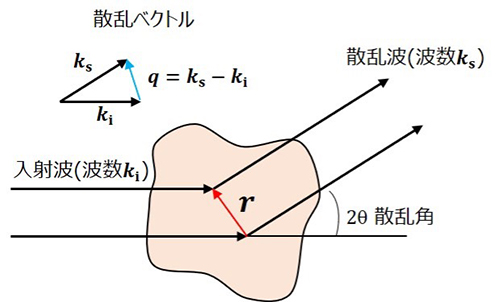 図1 散乱体からの散乱の模式図
図1 散乱体からの散乱の模式図 基本原理
小角散乱の基本的事項(干渉性散乱)について、簡単に述べます
1)-5)。図1のように散乱体に中性子(X線)が入射し、散乱体で散乱され、遠く離れた検出器で散乱波を観測します。入射波から散乱角(2θ)のところでは、散乱体中のあらゆる場所で散乱した波の重ね合わせを観測することになります。ここで、
r 離れた2点を通る波の間には行路差があり、その位相差は
r∙qで与えられます。
qは散乱ベクトルと呼ばれる量で入射波と散乱波の波数ベクトル
ki、ksの差で定義されます(
q=ks-ki)。したがって、散乱能密度
p(
r)分布(中性子の場合は散乱長密度B(
r)、X線の場合は電子密度ρ(
r))を持った試料からの散乱波の振幅(構造振幅)
F(
q)は
で与えられます。実際には、散乱光強度を観測するので、単位体積当たりの散乱強度
I(
q)は、
で与えられます。単位体積当たりの散乱長密度分布の自己相関関数、
を用いると、
散乱強度I(q)は散乱能分布p(r)の自己相関関数γ(r)のフーリエ変換として、
と書けます。
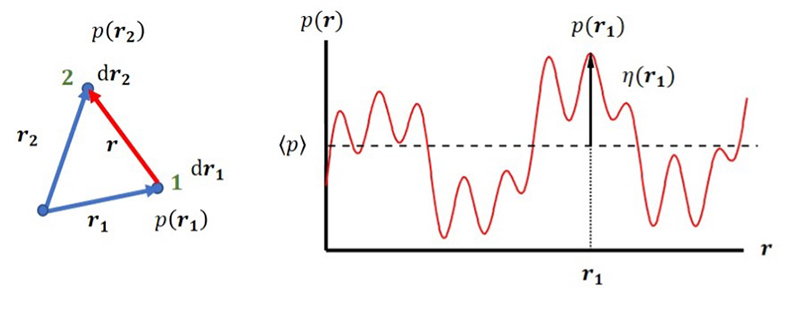 図2 (左)散乱体内部の位置ベクトルr1, r2における微少体積dr1, dr2をもった散乱要素と(右)散乱体内部の散乱能密度p(r)の空間的揺らぎη(r).
図2 (左)散乱体内部の位置ベクトルr1, r2における微少体積dr1, dr2をもった散乱要素と(右)散乱体内部の散乱能密度p(r)の空間的揺らぎη(r).
次に、散乱能分布の揺らぎη(
r)を考えます。これは散乱能の平均〈
p〉を用いて
と定義されます。図2のように、
r1での微小体積における平均散乱能密度〈
p〉からの揺らぎ(ずれ)をη(
r1 )とすると
(6),(7)式を(3)式に代入すると
となります。ここで規格化した自己相関関数γ
0 (
r)を
として導入すると、
となり、相関関数γ(
r)との関係が得られます。(10)式と(4)式から、散乱強度は
のように書けます。ここで、δ(
q)はクロネッカーのデルタ関数であり
q = 0の時に値を持つが実験上は透過光と重なるため、観測できないので省略できます。
したがって、散乱強度として観測されるのは、
試料中に存在する散乱能分布の揺らぎη(r)の自己相関関数のフーリエ変換であることが分かり、さらに
散乱強度は揺らぎの二乗平均〈η〉2に比例するという重要な結論が導かれます。
孤立粒子系の小角散乱
球状の微粒子(溶媒中に分散したエマルジョン粒子、ミセル粒子など)の解析として、微粒子の内部の密度が均一な球状粒子(半径
R、体積
Vs)の一個からの散乱振幅
F(
q)は次式で与えられます((1)式を計算することで得られます)。
ただし散乱体の散乱能を
ps、媒体の散乱能を
pmとしました。散乱関数
I(
q)は(13)式の二乗であたえられ、図3のような曲線が描かれます。図は半径
Rがガウス分布に従うとし、数平均
R=100nmとなる球状微粒子からの散乱関数を示しました。図中のσは標準偏差を表します。曲線は重なりを避けるため縦方向に10倍ずつシフトして表示しました。半径の分布が小さい場合、最初の谷の位置(
qR = 4.5)から、粒子の半径を見積もることができます。また散乱強度は半径の分布が大きくなると小角側の強度が大きくなっていること理解できます。つまり(13)式からもわかるように、散乱強度は体積の二乗に比例するため、半径の分布が大きいときには、大きな粒子からの散乱の寄与が顕著になります。他の粒子形状の例として、図4に棒状粒子(長さ
L 600nm、棒の半径
L 20nm)および薄い円盤(半径
L 300nm、厚み
h 20nm)からの散乱関数を示します。散乱体の形状に関して現れる散乱強度の
q依存性(べき乗則)について、棒状粒子からは
L-1≪
q≪
R-1において
I(
q)∝
q-1、円盤状粒子からは
R-1≪
q≪
h-1において
I(
q)∝
q-2が現れます。孤立粒子からの散乱のピーク位置(前述では谷の位置)は、形状に応じて表1のような関係があるので、粒子の半径や厚みを評価できます。
| 表1. 粒子形状と形状因子(粒子内干渉)のピーク位置qm,iの関係 |
| 半径Rの球状粒子 |
qm,i R=5.765, 9.111, 11.22 (i=1,2,3,⋯) |
| 半径Rの棒状粒子 |
qm,i R=4.98, 8.364, 11.46 (i=1,2,3,⋯) |
| 厚みhの板(円盤)状粒子 |
qm,i h=8.76, 15.14, 21.61 (i=1,2,3,⋯) |
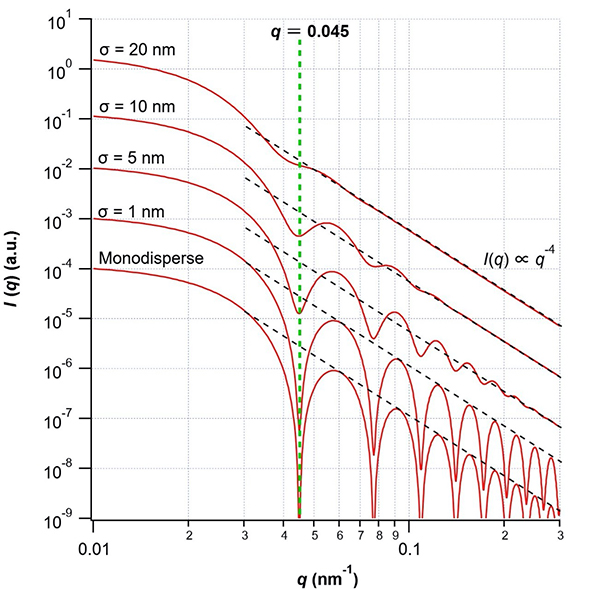 図3 球状微粒子からの散乱関数. 半径Rがガウス分布に従うとし, 数平均R=100nmとした図中のσは標準偏差を表す. 曲線は重なりを避けるため縦方向に10倍ずつシフトして表示した.
図3 球状微粒子からの散乱関数. 半径Rがガウス分布に従うとし, 数平均R=100nmとした図中のσは標準偏差を表す. 曲線は重なりを避けるため縦方向に10倍ずつシフトして表示した.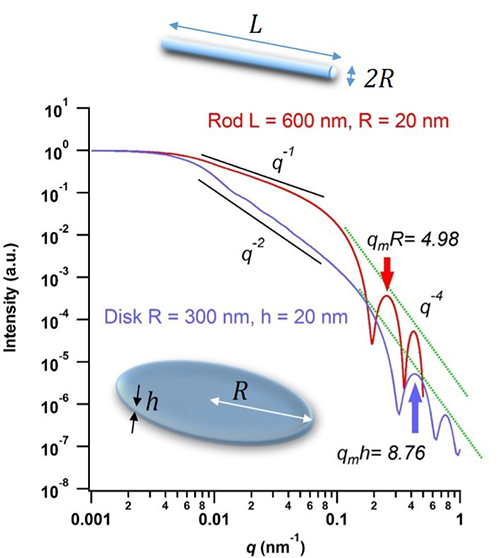 図4 棒状粒子(長さ600nm, 半径20nm)および円盤状粒子(半径300nm, 厚み20nm)からの散乱関数
図4 棒状粒子(長さ600nm, 半径20nm)および円盤状粒子(半径300nm, 厚み20nm)からの散乱関数
散乱体の大まかなサイズについて知りたいときには、Guinier近似がよく使われます。小角領域の散乱強度分布は粒子の回転半径
Rgにのみ依存するので、
Rgが等しい粒子は形状に関わらず、散乱強度分布は等価となり、Gauss関数で近似できます(Guinierの法則
2))。例えば、
qR≪1を満足する小角領域では、(13)式を二乗した散乱関数において、級数展開し整理すると次式のように書けます。
図5に球状粒子からの散乱曲線と(14)式のGuinierの法則による曲線を図示しました(半径20nm)。図からわかるように、
qが大きくなると破線は、青実線から逸脱します。右図は
q2に対してln{
I(
q)}をプロット(ギニエプロット)したものであり、右図の点線の傾きから粒子の回転半径が求まります。なお
qR ≪1ではGuinierの近似式は理論散乱強度と十分良好に一致します。前述しましたが、この
q領域では散乱は散乱体の回転半径にのみ依存し、形状には依存しません。一方、
qR≫1の極限(
q→∞)では、
I(
q)∝(
qR)
-4と近似できます。即ち散乱強度は
q-4に従って漸近的に減少します。これをPorodの法則
6)と呼び、散乱能密度が一様な散乱体の表面が平滑であることを意味します。
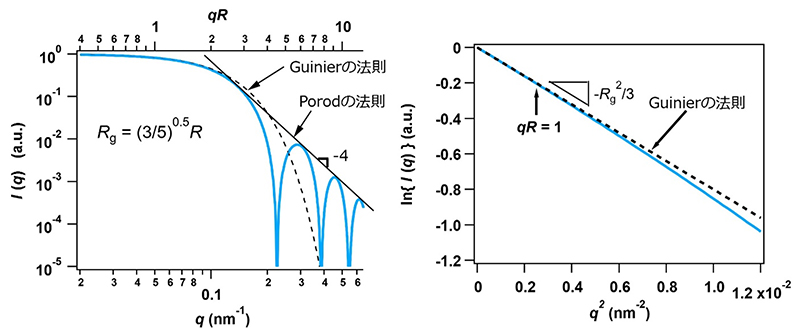 図5 (左)球状粒子からの散乱曲線(青実線)とGuinierの法則(黒破線)およびPorodの法則(黒実線)に従った漸近曲線. (右)Guinierプロット.
図5 (左)球状粒子からの散乱曲線(青実線)とGuinierの法則(黒破線)およびPorodの法則(黒実線)に従った漸近曲線. (右)Guinierプロット.コントラスト変調
中性子散乱法の大きな特長は、散乱長をマトリックス溶媒や観測散乱体の重水素化率を変化させることで、詳細な構造解析が可能になることにあります。図6に示すSurfactinと呼ばれる物質は有機溶媒中で会合し筒状の集合体を形成します。またこの系に適度な水を導入すると筒状の集合体内部に水を内包しウォーターチャネルを形成します
7)。実際に水が筒の内部にいるのか?中性子散乱結果から解析が可能となります。有機溶媒として重水素化シクロヘキサン(CHx)、水は軽水と重水と準備し、それぞれ同濃度になるように試料を調整します。その中性子散乱プロファイルを図7aにしまします(図中の
Aはプロファイルの重なりを防ぐために縦方向へのずらした際のシフト係数)。このとき、バックグランドとして透過率を考慮し溶媒や試料セル(窓材)からの散乱を差し引き、さらに非干渉性散乱を差し引いておきます。一見よく似た散乱プロファイルですが、
q = 2~3 nm
-1近傍の谷の位置が異なることが分かります。小角領域(0.5 < q < 1 nm
-1)では散乱強度の
q依存性に
q-1則が見られ棒状の集合体であることが分かります。実線は棒状集合体をコアー・シェル型の散乱長密度(Scattering Length Density; SLD)分布を持っていると仮定して計算した結果になります((15)式)。
ここで
J1は一次のベッセル関数、
RCはコアの半径、
RSは棒状集合体の半径(コアとシェル部を含む)、
SCはコアの断面積(π
RC2)、
SSは棒状集合体の断面積(π
RS2)、は
L棒状集合体の長さになります。ρ
C、ρ
S、ρ
0はそれぞれ、コア、シェル、溶媒のSLDとなります。さらに棒状集合体の半径は、どのような分布関数を用いてもよいのですが、ここではSchulz分布((16)式、
R0は半径の平均値、Γ(z)はガンマ関数、半径の平均二乗変移の平方根σ=1/(z+1)
0.5)を持たせて計算を行っています。
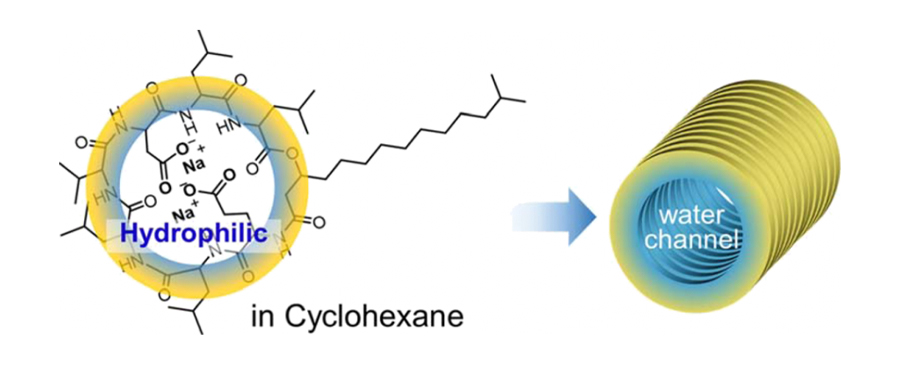 図6 Surfactin分子とその集合体のイメージ図(Langmuir 36, 7627-7633, (2020).)
図6 Surfactin分子とその集合体のイメージ図(Langmuir 36, 7627-7633, (2020).)
さて、図7aのプロファイルは、用いた水(軽水および重水)を変えても構造は不変であり、コントラストのみが変化した結果、得られたと考えられます。中性子散乱におけるSLDは図8に示す通りであり、軽水と重水では大きくSLDが変わることを利用します。図7bには棒状集合体の断面の中心からの距離に対して、SLDを描いたものになります。水を含まない系はコア・シェル型というより通常のシンプルな棒状集合体として観測され、軽水を用いた場合は、コアのSLDが小さくなり、重水を用いた場合はコアのSLDが大きくなることとなります。そのSLDプロファイルを用いて計算した結果が図7aの実線となります。これによりコア内部に水が存在することが示されます。
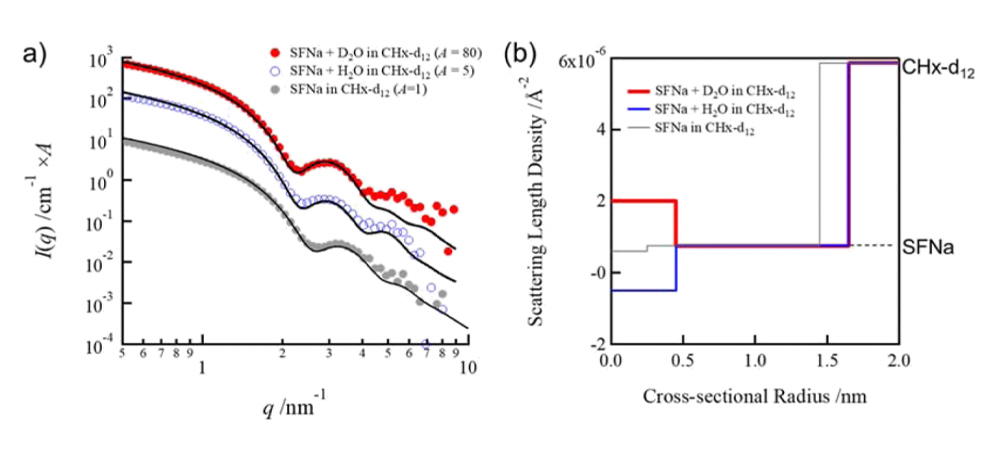 図7 (a) Surfactinのシクロヘキサン溶液からのSANSプロファイル(a). 赤;重水を添加した系, 青白抜き;軽水を添加した系, 灰色;水を含まない系. (b) 実験プロファイルを最もよく再現するSLDプロファイル.(Langmuir 36, 7627-7633, (2020).)
図7 (a) Surfactinのシクロヘキサン溶液からのSANSプロファイル(a). 赤;重水を添加した系, 青白抜き;軽水を添加した系, 灰色;水を含まない系. (b) 実験プロファイルを最もよく再現するSLDプロファイル.(Langmuir 36, 7627-7633, (2020).)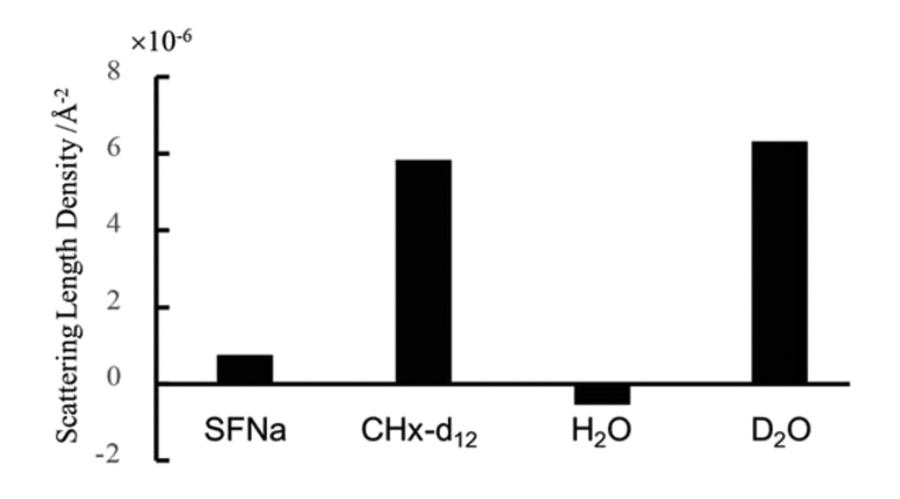 図8 散乱プロファイルの計算に用いたSLD (Langmuir 36, 7627-7633, (2020).)
図8 散乱プロファイルの計算に用いたSLD (Langmuir 36, 7627-7633, (2020).)
粒子間干渉効果
実在の系は、多数の粒子を含むことが多く、各粒子からの散乱波の干渉効果が無視できません。図9のように多粒子系において、この系の構造振幅
Ftは次式であたえられます。
FMはM番目の粒子の構造振幅(形状因子)です。散乱強度
I(
q)∝|
Ft|
2であり、次式で表されます。
全ての粒子が同じで球対称の時には、|
FM| = |
FJ| =|
F|なので、系の粒子数を
Nとすると
となります。第二項が粒子間干渉に依存する項であり、この場合粒子の相互配置のみに依存します。上式は粒子が
単分散で等方的という条件で形状因子|
F(
q)|
2と構造因子
S(
q)の積の形
と書くことができます。しかし、一般に形状因子と構造因子を分離することは難しく、粒子濃度が形状因子に影響を与える場合、粒子のサイズに分布がある場合、粒子間に配向相関がある場合など、分離は困難です。
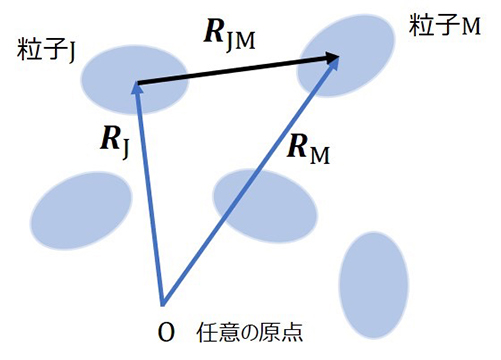 図9 粒子の集合体. RM, RJは任意の原点Oに対する位置ベクトル. RJMは粒子Jから粒子Mへの粒子間ベクトル.
図9 粒子の集合体. RM, RJは任意の原点Oに対する位置ベクトル. RJMは粒子Jから粒子Mへの粒子間ベクトル.Debyeの剛体球モデル
Debyeによって与えられた剛体球(Hard Sphere)
8)の散乱波、球と球が互いに侵入不可であること以外の相互作用を持たない粒子径系に適用されます。半径
RSの剛体球の散乱強度
I(
q)は
と記述されます。粒子の体積
VS=4π
RS3/3、
psおよび
pmはそれぞれ粒子の散乱能、マトリックスの散乱能とします。また系の粒子の体積分率を
VS/
v1としています。
図10に半径20nmの剛体球の集合体の|
Ft(
q)|
2(実線)および干渉因子(構造因子)
S(
q)(破線)を描きました。黒線は無限希釈(孤立粒子)の散乱関数に相当します((13)式 の二乗に等しい)。赤実線、青実線はそれぞれ、粒子の体積分率が0.05および0.12の場合であり、粒子間干渉効果が小角側で顕著に表れる(散乱強度が減少する)ことを示しています。
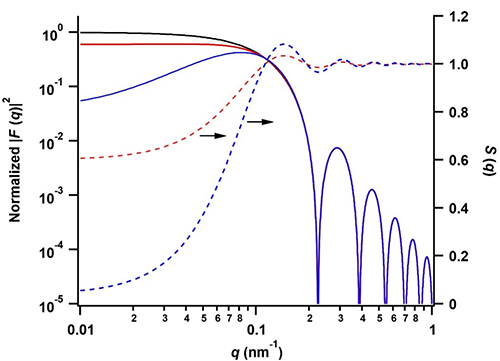 図10 Debyeの剛体球モデルの散乱関数. 縦軸はNVS2 (ps-pm)2で規格化した. 点線は構造因子(干渉因子)を表す. 黒実線は孤立粒子. 粒子の体積分率が0.05(赤)と0.12(青)の場合.
図10 Debyeの剛体球モデルの散乱関数. 縦軸はNVS2 (ps-pm)2で規格化した. 点線は構造因子(干渉因子)を表す. 黒実線は孤立粒子. 粒子の体積分率が0.05(赤)と0.12(青)の場合.ミクロ相分離構造からの小角散乱
ブロック共重合体が形成するミクロ相分離構造からの小角散乱パターンの解析にパラクリスタル理論に基づく散乱関数(次式)を利用した手法が用いられています
9)-10)。
F(
q)は粒子の構造振幅、
Nは粒子の総数、
Zkはパラクリスタルの格子因子、
Ickは0次の有限サイズのグレイン構造由来の散乱、
Nkは
k方向への粒子の数を表します。図11にブロック共重合体試料のミクロ相分離構造として、球状ミクロドメインがBCC格子上に配列した構造からの散乱、および、シリンダー状ドメインが六方充填した構造からの散乱を示します。図中の赤破線は孤立粒子(球およびシリンダー)からの散乱に対応するものとして示しました。黒破線は(24)式に基づいて計算したプロファイルであり、実験散乱プロファイルとよく一致しています
12)。球状ドメインの球状構造は明確ですが、BCC格子の長距離秩序は低く、一方、シリンダードメイン半径の大きさの分布が広いが、六方格子の長距離秩序性は高次の回折ピークが観測されるなど高いことなどが分かります。
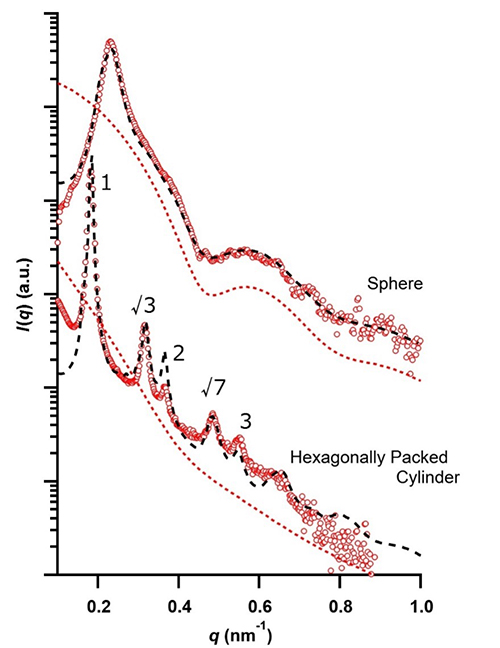 図11 ブロック共重合体における球状ミクロ相分離構造(上)とシリンダー状ミクロ相分離構造(下)からの散乱. 球状ドメインはBCC構造の一次ピークは{110}面反射であり
図11 ブロック共重合体における球状ミクロ相分離構造(上)とシリンダー状ミクロ相分離構造(下)からの散乱. 球状ドメインはBCC構造の一次ピークは{110}面反射であり,
その面間隔はd110 = 25.7nm. 球状ドメインの半径は10.1nm (σ= 1.14nm). 球状ドメインの体積分率は17.9%, 格子の乱れの程度を表すg因子(g=Δak/ak)は0.131として計算した. シリンダー構造の一時ピークは{10}面反射であり, その面間隔はd10 = 34.3nm. シリンダー半径は9.7nm(σ= 2.1nm), シリンダードメインの体積分率は21.7%, g因子は0.047として計算した.
全ては網羅できないですが、小角散乱法を利用するにあたり、参考となる文献
13)-17)も記しました。
参考文献
1)橋本竹治, 「X線・光・中性子散乱の原理と応用」講談社 (2017).
2)A.Guinier and G. Fournet, “Small-Angle Scattering of X-rays” John Wiley & Sons, New York (1955).
3)O. Glatter and O. Kratky eds, “Small-Angle X-ray Scattering” Academic Press (1982).
4)R. -J. Roe, “Method of X-ray and Neutron Scattering in Polymer Science” Oxford University Press, New York (2000).
5)松岡秀樹, 日本結晶学会誌41, 123-226 (1999).
6)G.Porod, Kolloid Z. 124, 83-114 (1951), ibid, 125, 51-57 (1952).
7)S.Kanazawa, K. Morimoto, E. Tabata, A. Okura, Y. Ikemoto, K. Yamamoto, L. de Campo, I.Akiba, Langmuir 36, 7627-7633, (2020).
8)P. Debye, Physik. Z., 28, 135-144 (1927).
9)T. Hashimoto, T. Kawamura, M. Harada, H. Tanaka, Macromolecules 27, 3063-3072 (1994).
10)H. Matsuoka, H. Tanaka, T. Hashimoto, N. Ise, Phys Rev. B. 36, 1754-1765 (1987).
11)H. Matsuoka, H. Tanaka, N. Iizuka, T. Hashimoto, N. Ise, Phys Rev. B. 41, 3854-3856 (1990).
12)G. Cui, M. Fujikawa, S. Nagano, K. Shimokita, T. Miyazaki, S. Sakurai, K. Yamamoto, Macromolecules 47, 5989-5999 (2014).
13)D.S.Sivia 著, 高中章朗 藤井康彦 共訳「X線中性子の散乱理論入門」森北出版 (2011).
14)J.Als-Nielsen, D. McMorrow著 “Elements of Modern X-ray Physics”, 雨宮慶幸, 高橋敏男, 百生敦 監訳、篠原佑也, 白澤徹郎, 矢代航 共訳,「X線物理学の基礎」講談社 (2012).
15)遠藤康夫「中性子散乱」朝倉書店 (2012).
16)柴山充弘, 佐藤尚弘, 岩井俊昭, 木村康之「光散乱法の基礎と応用」講談社 (2014).
17)「21世紀の小角散乱―放射光利用小角散乱実験技術の最先端」放射光学会誌 19, 337-453 (2006).


.jpg)
.jpg)
.jpg)
.jpg)

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)


.jpg)

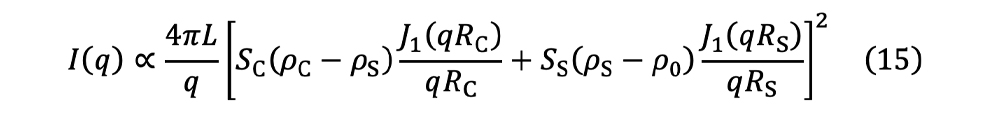
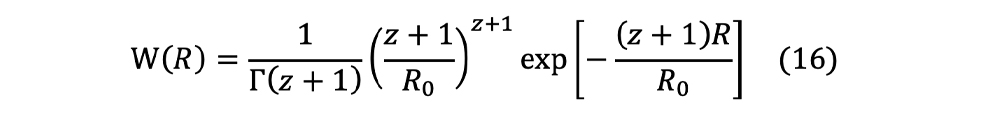



.jpg)
.jpg)
.jpg)
.jpg)

.jpg)

.jpg)
