執筆:鈴木大介(信州大学)
電気泳動光散乱法(Electrophoretic Light Scattering: ELS)は液中に分散しているコロイド粒子の電気泳動移動度やゼータ電位を求める手法
電気泳動光散乱法は(Electrophoretic Light Scattering: ELS)は、コロイド溶液に電場をかけた際に、等速で移動する分散質の速度を散乱される光から測定することで、電気泳動移動度(Electrophoretic Mobility: EPM)を求める手法です。例えば、EPMはSmoluchowskiの式を用いる事でゼータ電位に変換することができます。一般に、ゼータ電位は微粒子の表面電位と見なされるため、微粒子の分散状態を予測する事ができます。
測定できること
電気泳動移動度 / ゼータ電位 / ゼータ電位分布 / 等電点
原理
1. 電気泳動光散乱法とは
電気泳動光散乱法(Electrophoretic Light Scattering: ELS)は、コロイド溶液中の分散質の表面特性(帯電状態やゼータ電位等)を評価する手法です。官能基の解離やイオンの吸着などにより帯電したコロイド粒子が分散した系に対し、外部から電場を印加すると、コロイド粒子は自身の電荷の符号とは逆の電極に向けて移動します。その際に、コロイド粒子は溶媒から粘性抵抗を受けます。やがて、これら2つの力がつりあい、コロイド粒子は等速で動くようになります。この現象を電気泳動と呼びます(図1)。印加する電場が弱い場合(100 V/cm以下)、コロイド粒子の周囲に存在する拡散電気二重層と共に移動します。この電気泳動は第一種電気泳動と呼ばれており、この条件下では電気泳動速度
U と外部電場
E は比例します。一方で、印加する電圧が強い場合(2000 V/cm程度)、粒子の拡散電気二重層は粒子から外れ、粒子とは逆方向に移動します(第二種電気泳動)。一般的に、ELS測定を実施する際には第一種電気泳動が用いられています。
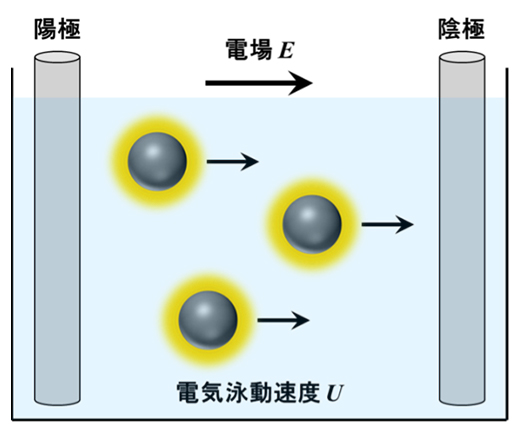 図1 電気泳動の原理
図1 電気泳動の原理 2. 測定原理
上述の様に、第一種電気泳動では、電気泳動速度は電場と比例関係にあります。この場合、電気泳動は電気泳動速度
U を電場
E で割った値(単位電場当たりの泳動速度)により特徴付けられます。この値を電気泳動移動度 (Electrophoretic mobility: EPM、μ) と言います。
EPMを求める手法は、顕微鏡で粒子が一定距離を移動するために要する時間を測定する顕微鏡電気泳動法
1)や、電気泳動中の粒子の結像を対物レンズによって回折格子面に投影し、格子から発生するパルスの周波数を解析する回転回折格子法
2)、コロイド分散液中に超音波をかけた際に発生する交流電圧を活用する超音波振動電位法
2)などがあります。今日では、操作性や測定精度、測定時間などの観点から、光散乱法と電気泳動法を組み合わせたELSが多く用いられています。
ELSでは、電場の印加により一定方向に等速で移動するコロイド粒子に対して、周波数ν
0の光を照射すると、散乱される光の周波数ν はドップラー効果により変化します(図2)。このドップラーシフト量
Δυと電気泳動速度
U の関係は式(2)のように表されます。
ここで
nは溶媒の屈折率、λ、θがそれぞれレーザー光の波長と、検出する散乱角を表します。得られた泳動速度に対して式(1)を適用する事で、EPMを算出することができます。
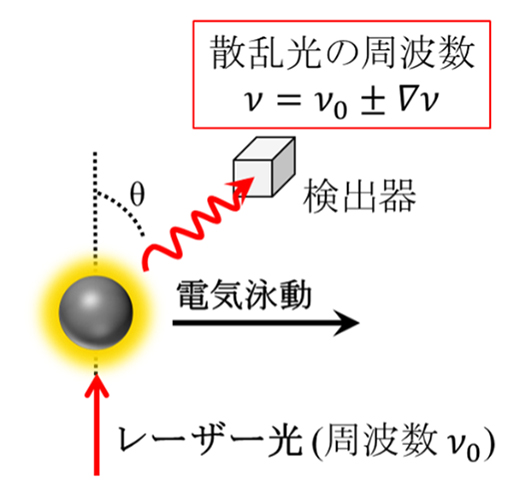 図2 光散乱電気泳動法
図2 光散乱電気泳動法 3. ゼータ電位の算出方法
電気泳動中のコロイド粒子には、粒子とともに移動するイオンと、その周りの溶液に取り残されるイオンが存在します。この境界をすべり面といいます(図3)。ゼータ電位は、このすべり面における電位として定義され、コロイド粒子の表面特性を理解する一つの指標となります。一般的にゼータ電位ζは、電気泳動移動度μの値をSmoluchowskiの式 (3)に代入する事で得られます。
ここでε
r、ε
0 はそれぞれ比誘電率と真空の誘電率、ηは溶媒の粘性率を表しています。ただし、電気泳動移動度をゼータ電位に変換する際には、適切な理論式を用いる必要があります。Smoluchowskiの式は、コロイド粒子が真球状であり、かつ電気二重層の厚さがコロイド粒子の大きさに比べて十分に大きい場合に適用します。例えば、電気二重層の厚さがコロイド粒子の大きさよりも十分に大きい場合(無塩系や有機溶媒中のコロイド粒子のゼータ電位測定の場合)、Smoluchowskiの式は適用できず、代わりにHückelの式 (4) が適用されます。
Smoluchowskiの式とHückelの式の間には2/3倍の違いがあります。
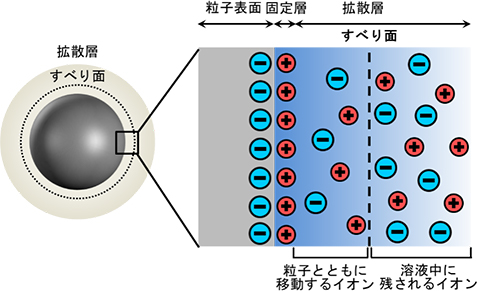 図3 コロイド粒子におけるすべり面とゼータ電位
図3 コロイド粒子におけるすべり面とゼータ電位
また、表面に高分子電解質層が存在するコロイド粒子(いわゆる柔らかい粒子)の場合では、ゼータ電位を議論することができません。これまで紹介したコロイド粒子とは異なり、柔らかい粒子は表面の高分子電解質層内に溶媒が侵入するため、明確なすべり面が存在しません。従って、ゼータ電位の物理化学的な意味が失われてしまいます。このような場合は、溶媒の侵入距離に関するパラメーターと、表面電荷層内の電荷密度を用いて表面特性が議論されます
3)。実際に、赤血球などの生体のコロイド粒子の表面特性は、前述の値を用いて特徴付けられ、議論が展開されています
4)。
その他にも、帯電した平板のゼータ電位を測定することも可能です。電場を印加した際、帯電した平板が存在する電解質溶液中にゼータ電位がほぼゼロであるコロイド粒子(トレーサー粒子)を分散させ、電場を印加します。この時、平板に接する電解質溶液の移動(電気浸透)の寄与によって、トレーサー粒子は電気泳動します。そのため、このトレーサー粒子のEPMを測定することによって、平板のゼータ電位を算出できます。また、この時の電気浸透速度の大きさは、(1)式と同じになります。そのため、帯電した平板のゼータ電位はSmoluchowski の式から算出することができます
5)。
コロイド粒子の表面特性は、学術的にも産業的にも重要なパラメーターです。扱っているコロイド粒子の特性を明確にし、適切なモデルを用いて表面特性を議論する事が重要です。
参考文献
1) 田中浩雄著 「顕微鏡電気泳動法によるゼータ電位の測り方(I)」紙パ技協誌 p29 (1979).
2) 古澤邦夫著 「ゼータ電位の測定」日本化学分析会誌ぶんせきp247 (2004).
3) H. Ohshima et al., J. Colloid Interface Sci. p512 (1993).
4) A. Hyono et al., Vox Sanguinis, (2008) p131.
5) Malvern, Application note: Determination of the zeta potential of the surface of PTFE (2016).
分析例・プロトコール

.jpg)
.jpg)

.jpg)
.jpg)
